Hierarchical Bayesian inversions

Posted on by — No Comments ↓
Monthly 2012 SF6 model-measurement uncertainties derived for daytime observations (blue) and nighttime observations (red) with errorbars corresponding to the 16th and 84th percentiles of the posterior distributions. The a priori value is shown by the black line.
Monthly 2012 SF6 model-measurement uncertainties derived for daytime observations (blue) and nighttime observations (red) with errorbars corresponding to the 16th and 84th percentiles of the posterior distributions. The a priori value is shown by the black line.

One of the main issues in trace gas inversions is in being able to correctly quantify the uncertainties in the system, as the inversion is very sensitive to these parameters.  These errors include a complete understanding of uncertainties in the instrument, uncertainties in the model and uncertainties in the a priori emissions.  In practice, being able to quantify these uncertainties is almost impossible.

To reduce the effect of errors in the assumptions made about these uncertainties, we have published a paper in Atmospheric Chemistry and Physics that details a hierarchical Bayesian inversion framework.  This framework is used to deduce time-varying uncertainties and correlation parameters.

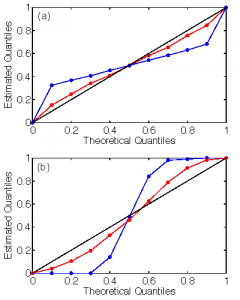
We show that the hierarchical method results in a more complete characterization of uncertainties, as shown by quantile-quantile plots blow.  To interpret these plots, a Q-Q plot on the 1:1 line means that the error statistics of the inversion are correctly capturing uncertainties in the system.  A Q-Q plot that is either an inverted S-curve or an S-curve indicates that the uncertainties specified in the inversion are under-constrained or over-constrained (that is the quantiles are either being over or under represented).  We show that inclusion of additional parameters in the inversion to accommodate “uncertainty in these uncertainties” results in a Q-Q plot that shifts toward the 1:1 line.

Quantile–quantile (Q–Q) plots of a hierarchical Bayesian inversion (red) and a non- hierarchical Bayesian inversion (blue) in which a priori emissions uncertainties used were (a) smaller than the true uncertainty (over-confident).
Quantile–quantile (Q–Q) plots of a hierarchical Bayesian inversion (red) and a non- hierarchical Bayesian inversion (blue) in which a priori emissions uncertainties used were (a) smaller than the true uncertainty (over-confident).

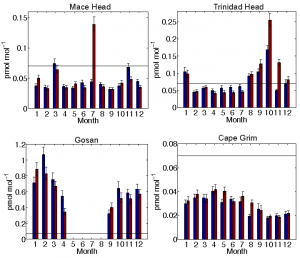
In our paper, we show how the hierarchical system can lead to more accurate emissions estimates. We present case study of sulfur hexafluoride emissions, and specifically highlight East Asian emissions derived with different estimates of model uncertainty.  The differences are considerable, and emphasizes the importance of characterizing uncertainties properly.

national_emissions
National emissions derived using three methods: (1) hierarchical Bayesian (HB) inversion (blue); (2) non-hierarchical Bayesian inversion (NHB) with model-measurement uncertainties that include a model error (red); and (3) non-hierarchical Bayesian inversion in which no model error was included (green). A priori emissions are shown as black bars, and uncertainties reflect the 16th to 84th percentiles of the posterior national emissions. The asterisk (*) refers to countries in which emissions were derived for only a fraction of the country. For clarity, the inset shows a magnified view of countries with relatively smaller emissions.

Leave a Reply